Meereismodellierung
Dieser Bereich des Meereisportals gibt einen Überblick darüber, wie Meereis in Computermodellen simuliert wird und welchen wissenschaftlichen Fragen man mit Meereismodellen nachspüren kann.
Neben der Meereisbeobachtung ist die Modellierung von Meereis ein wichtiges Instrument, die physikalischen Grundlagen der Meereisentwicklung zu untersuchen und dadurch die Wechselwirkungen mit der Atmosphäre und dem Ozean sowie die Ursachen für Veränderungen besser zu verstehen. Mit einem Computermodell ist es darüber hinaus möglich, Vorhersagen über zukünftige Entwicklungen des Meereises unter sich ändernden Klimabedingungen abzuleiten.
Um einen komplexen Gegenstand wie das Meereis und seine Wechselwirkung mit der Umwelt nachvollziehen, verstehen und vorhersagen zu können, genügt es nicht, nur gründliche Messungen durchzuführen und aus diesen die physikalischen Gesetzmäßigkeiten direkt abzuleiten. Vielmehr muss es gelingen, die vermuteten physikalischen Gesetzmäßigkeiten über mathematische Gleichungen in Computermodelle zu übersetzen und die wesentlichen beobachteten Abläufe damit mathematisch zu beschreiben. Stellt man dann fest, dass die Simulationen eines Modells mit den Beobachtungen nicht in Einklang zu bringen sind, ist klar, dass die vermuteten Gesetzmäßigkeiten falsch oder zu ungenau beschrieben sind, ihre Übersetzung ins Modell fehlerhaft ist oder wichtige Prozesse fehlen. Oft geben die Art und Weise der Abweichungen gute Hinweise darauf, wie das Modell verbessert werden kann. Es folgen dann eine Reihe von Modellanpassungen und neuen Simulationen, deren Ergebnisse nach Möglichkeit immer besser zu den Beobachtungen passen.
Auch am vorläufigen Ende eines solchen Entwicklungsprozesses ist selbstverständlich kein Modell perfekt. Schon George Box, britischer Wissenschaftler, schrieb 1976 sinngemäß, dass alle Modelle falsch, manche jedoch nützlich sind. Bei der gerade beschriebenen Vorgehensweise gelangt man schließlich dennoch zu einem ausreichend realistischen Modell, um einerseits mit größerer Überzeugung sagen zu können, dass man die wesentlichen Prozesse verstanden hat. Andererseits kann ein solches Modell nun dazu verwendet werden, wissenschaftlichen Fragen über das Meereis und dessen Rolle im Klimasystem sowie über seine zukünftige Entwicklung nachzugehen.
Folgendes Video verdeutlicht, welchen erstaunlichen Detailgrad eine Computersimulation des arktischen Meereises im Wechsel der Jahreszeiten haben kann.
In diesem Bereich des Meereisportals möchten wir die grundlegende Herangehensweise in der Meereismodellierung erklären, eine Einführung in die Funktionsweise von Meereismodellen geben, um anschließend einige Anwendungsbeispiele vorzustellen. Wenn Sie mehr über Modelle erfahren wollen, die das gesamte Erdsystem und das Klima simulieren, empfehlen wir Ihnen den Artikel „Sechs Fragen an einen Klimamodellierer".
Wie funktioniert ein Meereismodell?
Möchte man die Entstehung, die Entwicklung und das Schmelzen der auf dem Ozean schwimmenden Eiskruste simulieren, so kann man zwei grundlegende Arten von Vorgängen unterscheiden: thermodynamische und dynamische Prozesse. Letztere sind solche, die direkt mit der großräumigen Bewegung des Meereises zusammenhängen. Im Folgenden betrachten wir jedoch zunächst die thermodynamischen Prozesse, jene also, die auch ohne horizontale Bewegungen vonstattengehen. Dazu stellen wir uns vor, dass wir uns mit einer Eisscholle und ihrer Umgebung mitbewegen, je nachdem, wie sie auf dem Ozean in die eine oder andere Richtung bewegt wird. Anschließend beleuchten wir die Rolle von Bewegungen und wie diese auf Rechengittern modelliert werden. Schließlich beschreiben wir die Kombination mit anderen Modellkomponenten, beispielsweise in Klimamodellen, sowie die Optimierung und Weiterentwicklung von Meereismodellen.
Eine betrachtete Eisscholle und ihre Umgebung sind zunächst der Wirkung thermodynamischer Vorgänge ausgesetzt. Hierzu zählen beispielsweise die wärmende oder kühlende Wirkung von Sonnenlicht und Wärmestrahlung (thermische Ein- und Abstrahlung), der direkte Wärmeaustausch mit der Luft oder dem Ozean, die Wärmeleitung innerhalb des Eises und der Schneeauflage, die resultierenden Gefrier- und Schmelzprozesse, die Bildung von Schmelztümpeln und viele weitere Vorgänge.
Ob und mit welchem Detailgrad diese Vorgänge im Modell dargestellt werden, variiert stark. Generell können auf absehbare Zeit keine einzelnen Schollen und ihre räumliche Anordnung großräumig – zum Beispiel für die gesamte Arktis – simuliert werden, da dies die Möglichkeiten selbst modernster Hochleistungsrechner übersteigen würde. Stattdessen werden einzelne Schollen gemeinsam mit ihrer Umgebung, welche viele ähnliche Schollen umfasst, in einer sogenannten Gitterzelle zusammengefasst. Ein solche Gitterzelle hat meist eine rechteckige Form und ist typischerweise 10 km mal 10 km groß, kann jedoch je nach Modellauflösung auch deutlich größer oder kleiner und drei- statt viereckig sein. Für diese Gitterzelle werden im Modell nun Flächenanteile definiert, im einfachsten Fall ein Flächenanteil mit und einer ohne Meereis (Abbildung rechts). Dabei wird nicht festgelegt, wo genau innerhalb der Gitterzelle welcher Flächenanteil vorliegt. Der Anteil mit Meereis an der Gesamtfläche der Gitterzelle ist die sogenannte Meereiskonzentration – eine der wichtigsten Größen nicht nur in jedem Meereismodell, sondern auch bei der Beobachtung von Meereis durch Satelliten.

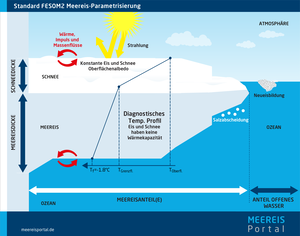
Die thermodynamischen Vorgänge wirken nun einerseits innerhalb der jeweiligen Flächenanteile: Zusätzliches Gefrieren sorgt für ein Anwachsen der Eisdicke, Schneefall für eine Erhöhung der Schneeauflage, und so weiter. Andererseits können die thermodynamischen Vorgänge aber auch zu einer Änderung der Flächenanteile führen. So würde beispielsweise eine Eisbildung im Anteil ohne Meereis dazu führen, dass dieser eben nicht mehr eisfrei wäre. Um diesen Widerspruch zu verhindern, führt das neu gebildete Eis zu einer Veränderung der Flächenanteile: Der Anteil mit Meereis nimmt auf Kosten des eisfreien Anteils zu. Der Teufel steckt dabei jedoch im Detail. Im Folgenden wird exemplarisch auf dieses Detail eingegangen, um einen Eindruck zu geben, wie solche Vorgänge in Meereismodellen dargestellt – parametrisiert – werden können.
Zunächst wird angenommen, dass das neugebildete Eis grundsätzlich eine bestimmte Dicke aufweist, zum Beispiel einen halben Meter. Es soll aber kein neuer Flächenanteil extra für dieses neugebildete Eis eingeführt werden, da die Zahl der zu berücksichtigenden Flächenanteile sonst immer größer würde. Stattdessen wird das neugebildete Eis mit dem Anteil bestehenden Eises kombiniert. Die resultierende Eisdicke ergibt sich durch Mittelung beider Anteile, so dass die Zunahme des Eisvolumens insgesamt mit der Menge neu gebildeten Eises übereinstimmt. Dabei ist es durchaus plausibel, nicht anzunehmen, dass der gesamte zuvor eisfreie Bereich einfach mit einer dünnen Schicht überfriert. Stattdessen lässt sich in der Natur beobachten, dass sich Eiskristalle durch Wasser- und Eisbewegungen typischerweise an den Rändern bestehender Eisschollen sammeln und erst dort neues zusammenhängendes Eis bilden.
In komplexen Meereismodellen werden viele physikalische oder auch biogeochemische Vorgänge zusätzlich und in größerem Detail betrachtet (Abbildung links). So wird der Flächenanteil mit Meereis weiter unterteilt in Anteile verschiedener Eisdicke. Neues, im offenen Wasser gebildetes Eis landet in diesem Fall zuerst in der dünnsten Eisdickenklasse. Die Anteile in den verschiedenen Eisdickenklassen können durch thermodynamische Vorgänge, also insbesondere Gefrier- oder Schmelzprozesse, allmählich in dickere oder dünnere Klassen überführt werden. Es gibt jedoch eine weitere wichtige Art von Prozessen, welche die Form des Meereises entscheidend beeinflusst: Bewegungen, bei denen sich verschiedene Bereiche der Eisfläche gegeneinander verschieben.
Bevor die Einflüsse von Bewegungen und weiterer Vorgänge betrachtet werden, wird im Folgenden die Funktionsweise eines Meereismodells anhand einer einfachen mathematischen Gleichung veranschaulicht. Dabei soll auf eine allzu mathematische Darstellung verzichtet werden. Da man die Physik der betrachteten Vorgänge jedoch nur über solche Modellgleichungen im Computer berechnen machen kann, soll hierfür ein Beispiel gegeben werden. Die Veränderung der Meereiskonzentration kann wie folgt beschrieben werden:
Meereiskonzentration(t + 30 Minuten) = Meereiskonzentration(t) + Zuwachs +/- Rest
Wenn wir also die Meereiskonzentration zu einem Zeitpunkt t kennen, ergibt sich aus dieser Gleichung die Meereiskonzentration zum Zeitpunkt 30 Minuten später (t + 30 Minuten), indem zunächst der Zuwachs durch Eisneubildung im offenen Wasser über diesen Zeitraum hinzugefügt wird. 30 Minuten sind hierbei ein exemplarischer aber realistischer Modellzeitschritt. Hinter dem Zuwachs verbirgt sich eine weitere Gleichung, die die in Abschnitt Meereis in der Gitterzelle geschilderten Vorgänge abbildet: Je nachdem, wie kalt die Luft ist, die in Kontakt mit dem am Gefrierpunkt befindlichen Wasser steht, bildet sich innerhalb von 30 Minuten eine bestimmte Menge an Eiskristallen. Hierbei wird angenommen, dass sich diese Eiskristalle in einer 0,5 Meter dicken Schicht sammeln, woraus sich wiederum errechnen lässt, welchen Zuwachs die Meereiskonzentration erfährt. Diese Annahme ist natürlich stark vereinfachend, hat sich aber in der Modellierung bewährt. Außerdem enthält diese Gleichung einen Rest, der sich durch andere Vorgänge ergibt, zum Beispiel durch Eisbewegungen (siehe Meereis in Bewegung) oder wenn wärmeres Wasser zum Schmelzen am Rand der Schollen führt.
Natürlich muss eine weitere Gleichung die Entwicklung der Eisdicke beschreiben und noch weitere Gleichungen müssen für jede weitere Größe aufgestellt werden, die zusammen den Eiszustand im Modell beschreiben. Anhand dieser Gleichungen hangelt sich das Modell nun Schritt für Schritt in der Zeit voran, angefangen an einem vorgegebenen Anfangszustand, der z. B. aus Beobachtungen abgeleitet wird. In modernen globalen Meereis- und Klimamodellen müssen in jedem Zeitschritt sehr viele Gleichungen auf Millionen von Gitterzellen berechnet werden. Um das in akzeptabler Zeit zu schaffen, werden Hochleistungsrechner wie der am Deutschen Klimarechenzentrum (DKRZ) in Hamburg verwendet.
Neben den temperaturgetriebenen (thermodynamischen) Prozessen wirken auch horizontale Bewegungen und Verschiebungen als Kräfte auf die Eisschollen ein. Diese werden als Dynamik des Meereises bezeichnet. Der Begriff Dynamik bedeutet ursprünglich Kraft, meint im hier beschriebenen Zusammenhang aber die Bewegung und das Fließverhalten (Rheologie des Eises). Es wird zunächst weiterhin eine Gitterzelle im Meereismodell betrachtet, die der großräumigen Bewegung des Eises folgt. Was geschieht nun, wenn die Winde oder die Meeresströmungen das Eis auseinandertreiben? In einer solchen Situation (hier spricht man von Divergenz) kann man sich vorstellen, dass einfach die Bereiche offenen Wassers größer werden.
Komplizierter wird es, wenn das Eis zusammengetrieben wird (Konvergenz der Bewegung). Zuerst werden möglicherweise noch vorhandene Bereiche offenen Wassers kleiner: die Meereiskonzentration nimmt zu. Erreicht diese jedoch fast 100 %, bauen sich im Eis Spannungen auf, die bei ausreichend starken Schubkräften dazu führen können, dass sich Schollen aufeinander schieben. Nehmen die Spannungen weiter zu, können auch innerhalb geschlossener Eisdecken Bruchlinien entstehen, an denen sich nun Presseisrücken auftürmen. Die Meereisdicke nimmt bei zusammenlaufender (konvergenter) Eisbewegung also nicht überall gleichermaßen zu, sondern sehr konzentriert entlang einzelner Bruchlinien. Auch Scherspannungen, wie sie zum Beispiel entstehen können, wenn Meereis an einer Küste festgefroren ist, das Eis zugleich jedoch durch Wind oder Strömung entlang der Küste angeschoben wird, können zu Brüchen im Eis führen. Diese ermöglichen dann wiederum die Bildung von Presseisrücken einerseits und Rinnen offenen Wassers andererseits.
In einfachen Modellen mit nur einer Eisdickenklasse können solche Vorgänge nicht gut abgebildet werden, da nur eine mittlere Eisdicke nachgehalten wird. Es bleibt dem Modell bei konvergenter Eisbewegung also nichts anderes übrig, als so zu tun, als nähme die Meereisdicke gleichmäßig zu. In komplexen Meereismodellen hingegen kann diesen Vorgängen Rechnung getragen werden, indem Flächenanteile mit dickem Eis auf Kosten dünnerer Eisklassen vergrößert werden.
Betrachtet man nur relative Bewegungen des Eises innerhalb einer Gitterzelle, so wird angenommen, dass die Gitterzelle einfach der großräumigen Eisbewegung folgt. Um das Meereis und seine räumliche Verteilung jedoch ganzheitlich simulieren zu können, muss auch die großräumige Bewegung des Eises vom Modell selbst berechnet werden. Zentrale Rollen kommen dabei dem Wind und der Meeresströmung zu, wobei in den meisten Gebieten mit Meereis der Wind den Hauptantrieb liefert und der Ozean die Bewegung bremst. Welche Kraft ein bestimmter Wind oder eine bestimmte Strömung verursacht, wird dabei in Modellen über bestimmte Parameter, sogenannte Transferkoeffizienten, beschrieben. Meist wird angenommen, dass die übertragene Kraft proportional zur relativen Wind- oder Strömungsgeschwindigkeit ist. Eine doppelt so hohe relative Windgeschwindigkeit führt also zu einer doppelt so hohen Schubkraft.
Da das meist nur etwa ein oder zwei Meter dicke Meereis recht schnell auf diese Kräfte reagiert, stellt sich zügig ein ungefähres Kräftegleichgewicht ein, welches zusätzlich durch die Corioliskraft und eine mögliche leichte Neigung der Meeresoberfläche beeinflusst wird. Ändert sich nun die Windrichtung oder -stärke, so wird das Eis in der Gitterzelle entsprechend beschleunigt, gebremst oder umgelenkt. Doch was geschieht, wenn das Eis in ein Gebiet gelangt, wo bereits Eis mit hoher Meereiskonzentration vorliegt und nicht gleichermaßen ausweicht, oder wenn sich die Gitterzelle einer Küste nähert? Spätestens jetzt kann die Gitterzelle nicht mehr isoliert betrachtet werden, sondern es muss das Zusammenspiel mit der weiteren Umgebung, also den benachbarten Gitterzellen, berücksichtigt werden.
Innerhalb einer Gitterzelle wirken Schubkräfte, Spannungen und Verformungen im und auf das Eis. Diese Vorgänge können jedoch auch die großräumige Bewegung des Eises entscheidend beeinflussen, und zwar überall dort, wo das Meereis dicht gepackt ist, also eine hohe Meereiskonzentration vorliegt. Hier können Spannungen im Eis schnell über große Entfernungen wirken. Schiebt der Wind beispielsweise das Meereis in Richtung Küste, ohne dass größere Rinnen oder andere offene Wasserflächen dazwischen liegen, entstehen Spannungen im Eis, die sehr schnell von Gitterzelle zu Gitterzellen weitergeleitet werden und sich über mehrere 100 km erstrecken können. So ergibt sich auch über mehrere Gitterzellen hinweg eine interne Eis-Kraft, die der Schubkraft des Windes entgegenwirkt und das Eis an Ort und Stelle hält.
In Bereichen hoher Meereiskonzentration halten sich also nicht mehr einfach die Schubkräfte von Luft und Wasser die Waage, wie bei einer frei driftenden Scholle. Stattdessen entstehen interne Spannungen, die zu einem maßgeblichen Faktor in der Bewegungsgleichung werden. Und da die Spannungen schnell über große Entfernungen übertragen werden, müssen im Modell die Bewegungsgleichungen vieler Gitterzellen gleichzeitig gelöst werden. Das ist ohnehin notwendig, wenn nicht nur das Schicksal einer einzelnen Scholle und ihrer direkten Umgebung betrachtet und simuliert werden soll, sondern die Entwicklung des Meereises in größerem Zusammenhang – zum Beispiel in der gesamten Arktis oder Antarktis.
Hierfür gibt es zwei grundsätzliche Strategien, ein ganzes Gitter bestehend aus einer Vielzahl von Zellen zu simulieren. In beiden Varianten teilt man zunächst das Gebiet, zum Beispiel die Arktis, in ungefähr gleich große Gitterzellen auf. Bei der ersten Strategie („Lagrang’sche Methode“) bewegt sich nun im Laufe der Zeit jede der Gitterzellen mit der großräumigen Bewegung des Eises mit, genauso, wie wir es bereits für eine einzelne Gitterzelle angenommen haben. Das hat den Vorteil, dass die Informationen, die zum Beispiel in der Eisdickenverteilung gespeichert sind, automatisch über die Zeit weitergegeben werden – mit jeder Gitterzelle wird das Schicksal eines konkreten Stücks Meereis verfolgt. Bei der zweiten Strategie („Eulersche Methode“) sind die Berechnungspunkte (Gitterzellen) dagegen ortsfest und die Eigenschaften des Eises müssen von Zelle zu Zelle weitergegeben werden, je nach Bewegung.
Das sich mit der Eisbewegung mitbewegende Modellgitter, der sogenannte Lagrangesche Ansatz für ein Meereismodell, ist physikalisch elegant, führt aber auch zu erheblichen technischen Schwierigkeiten, da sich das Gitter mit der Zeit verformt und in einigen Bereichen immer mehr verdichtet, in anderen hingegen immer spärlicher wird (siehe im Abschnitt Von der einzelnen Gitterzelle zum ozeanweiten Modellgitter verlinktes Video).
Bei regional begrenzten Modellen ergeben sich zusätzlich leicht einzusehende Probleme an den Grenzen des Modellgebiets. Daher müssen größer werdende Gitterzellen geteilt und kleiner werdende Gitterzellen kombiniert, Gitterzellen neu erzeugt und entfernt, oder alle Gitterzellen von Zeit zu Zeit ganz und gar neu definiert werden. Darüber hinaus sind die Daten über den Zustand der Atmosphäre und des flüssigen Ozeans, die entweder von anderen Modellkomponenten interaktiv berechnet werden oder aus anderen Datensätzen stammen, allgemein auf zeitlich unveränderlichen Gittern gegeben. Wenn sich nun das Meereis-Gitter ständig verformt, muss auch zu jedem Zeitpunkt neu berechnet werden, auf welche Datenpunkte jede einzelne Gitterzelle zugreifen muss.
Zwar gibt es solche Lagrange‘schen Meereismodelle, bei denen das Rechengitter stets der Bewegung des Eises folgt (z. B. Rampal et al. 2016). Deutlich einfacher und daher üblicher sowie meist auch weniger rechenintensiv ist es jedoch, ein zeitlich unveränderliches Gitter zu definieren, so wie es in fast allen Atmosphären- und Ozean-Gittermodellen gehandhabt wird. Bereits das erste großräumige Meereismodell, das sowohl die Thermodynamik als auch die Dynamik von Meereis so beschrieben hat, folgte diesem sogenannten Eulerschen Ansatz eines ortsfesten Gitters (Hibler 1979). Dabei entfallen die oben genannten Schwierigkeiten. Stattdessen muss nun jedoch dafür Rechnung getragen werden, dass die Eigenschaften des Eises, also die Meereiskonzentration etc., mit der großräumigen Bewegung von Gitterzelle zu Gitterzelle weitergegeben werden. Driftet das Eis beispielsweise innerhalb eines 30-minütigen Modellzeitschritts von Zelle A zu Zelle B, so dass 10 % von Zelle B nun Eis enthält, das sich zuvor in Zelle A befand, so ergibt sich im einfachsten Fall der neue Zustand in Zelle B aus dem entsprechend gewichteten Mittel der vorherigen Zustände in den beiden Zellen:
Eiszustand(Zelle B, Zeit t + 30 Minuten ) = 90 % * Eiszustand(Zelle B, Zeit t ) + 10 % * Eiszustand (Zelle A, Zeit t ).
Dabei stecken hinter „Eiszustand“ mehrere bis viele einzelne Größen, die diesen Zustand im Modell beschreiben: je nach Komplexität des Modells (vgl. Abbildung) die Meereiskonzentration, die Flächenanteile der verschiedenen Dickenklassen, die jeweilige Schneeauflage, die Temperatur und der Salzgehalt des Eises und des Schnees in verschiedenen Tiefen, und so weiter. Es ergeben sich also viele einzelne Gleichungen. Entsprechende Gleichungen müssen natürlich für Zelle A und für alle anderen Zellen aufgestellt und gelöst werden. Auch lässt sich leicht einsehen, dass in einem zweidimensionalen Modell die Eiszustände mehrerer Nachbarzellen in diese Gleichungen eingehen, wie in der Abbildung veranschaulicht, und die Anteile (im Beispiel 90 % und 10 %) in jedem Zeitschritt abhängig vom aktuellen Bewegungszustand des Eises neu berechnet werden müssen. Dennoch lässt sich dieser Vorgang der Advektion vergleichsweise leicht ins Computermodell einbauen. Ein Nachteil der Eulerschen gegenüber der Lagrange‘schen Methode ist, dass die Advektion nach und nach zu numerischer Diffusion, das heißt, zu einer gewissen Vermischung des Eiszustandes zwischen den Gitterzellen, führt. Es gibt numerische Methoden, um das Problem dieser unrealistischen Vermischung zu verringern, gänzlich zu vermeiden ist es jedoch nicht.
Meereis als Teil des Klimasystems
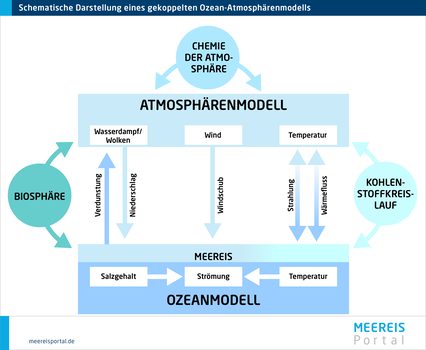
Das Meereis ist eine wichtige Komponente im Klimasystem und steht in vielfacher Wechselwirkung mit dem darunterliegenden Ozean und der darüberliegenden Atmosphäre. Um das Verhalten des Eises über die Zeit und seinen Einfluss auf die Klimabedingungen der Erde möglichst wirklichkeitsgetreu zu simulieren, ist es sinnvoll, ein Meereismodell mit anderen Teilmodellen für den Ozean und die Atmosphäre zu koppeln und so aus Einzelteilen ein größeres Ganzes zu schaffen. Hier erklären wir Ihnen, wie das funktioniert.
Meereismodelle beschreiben komplexe Zusammenhänge der Eiszu- und -abnahme, die durch thermodynamische und dynamische Prozesse erfolgen. Im Prinzip kann ein Meereismodell daher auch ungekoppelt, also ohne weitere interaktive Modellkomponenten, verwendet werden. Dazu müssen die Randbedingungen oberhalb und unterhalb des Eises – also der Wind, die Lufttemperatur, die Einstrahlung, der Niederschlag, sowie die Temperatur, der Salzgehalt und die Strömung des Wassers – einschließlich ihres zeitlichen Verlaufs aus bestimmten Datensätzen fest vorgeschrieben werden. Für die Atmosphäre stammen solche Daten meist aus sogenannten Reanalysen, die von operationellen Wettervorhersagezentren im Zuge ihrer täglichen Verarbeitung weltweiter Messdaten in Kombination mit Wettervorhersagemodellen routinemäßig erzeugt werden. Für den Ozean gibt es zwar technisch auf ähnliche Art, also durch Datenassimilation, erzeugte Reanalyse-Datensätze. Diese sind jedoch gerade in den eisbedeckten Polargebieten besonders fehleranfällig, da hier die Messdaten besonders lückenhaft sind.
Ein weiterer Grund, den Zustand des flüssigen Ozeans nicht fest vorzugeben ist, Inkonsistenzen zwischen dem Eis- und dem Ozeanzustand zu vermeiden. Stelle man sich beispielsweise vor, eine größere Menge Meereis gerät in ein Gebiet mit erhöhten Meerestemperaturen. In der Realität würde das Eis beginnen zu schmelzen, dabei das umgebende Wasser abkühlen und dadurch die Schmelzrate verlangsamen. Im ungekoppelten Meereismodell fehlt diese Abkühlung und damit die Verlangsamung des Schmelzens. Gebiete im ozeanischen Datensatz mit Wassertemperaturen nahe dem Gefrierpunkt des salzigen Ozeans von ca. -1,8 °C lassen die Eisbildung hingegen zu, sobald die Lufttemperaturen noch tiefer liegen; bei nur wenig höherer Meerestemperatur wird die Eisbildung hingegen sehr effektiv verhindert. Im Ergebnis spiegelt die vom ungekoppelten Modell simulierte Eisverteilung lediglich die bei der Erzeugung des ozeanischen Datensatzes angenommene oder simulierte Eisverteilung wider.
Daher ist es meist sinnvoller und üblicher, ein Meereismodell gekoppelt mit einem ebenfalls interaktiven Ozeanmodell zu betreiben. Dabei tauschen beide Modellkomponenten ständig Informationen über ihren aktuellen Zustand aus, so dass sie gemäß den simulierten Gesetzen der Physik konsistent aufeinander reagieren können. Oft werden Meereismodelle auch von Anfang an als Teil eines Ozeanmodells entwickelt, so dass keine externe Kopplung unabhängiger Modellkomponenten mehr nötig ist. Dies hat in der Regel den praktischen Nebeneffekt, dass beide Komponenten auf demselben Modellgitter beschrieben werden, wodurch die sonst beim Austausch zwischen verschiedenen Gittern notwendigen Zuordnungen und Umrechnungen entfallen.
Inkonsistenzen zwischen einzelnen Modellkomponenten des Erdsystems können auch auftreten, wenn ein Eis-Ozean-Modell mit vorgeschriebenen atmosphärischen Daten aus Reanalysen angetrieben wird, statt auch hierfür eine interaktive Modellkomponente zu verwenden. In der Tat ergeben sich auch hier solche Effekte - die zu simulierende Eisverteilung ist zumindest zum Teil schon durch das Muster der atmosphärischen Temperaturen bestimmt. Dennoch ergeben sich bereits viele interessante Anwendungen für Eis-Ozean-Modelle.
Ein weiteres, drängendes Thema, bei denen Meereismodelle eine wichtige Rolle spielen – ist der Klimawandel. Hier ergibt sich eine noch wichtigere Einschränkung für die Verwendung eines Eis-Ozean-Modells ohne interaktive Atmosphäre: das offensichtliche Fehlen beobachtungsbasierter Datensätze der zukünftigen Atmosphäre. Hierfür werden also auch vollständig gekoppelte Atmosphäre-Eis-Ozean-Modelle gebraucht. Bei solchen Klimamodellen ist die Kopplung in beiden Richtungen von großer Bedeutung. Nur so kann zum Beispiel die verstärkende Eis-Albedo-Rückkopplung, bei der ein erwärmungsbedingter Meereisrückgang zu einer vermehrten Absorption von Sonnenstrahlung und somit zu weiterer Erwärmung führt, physikalisch konsistent simuliert werden.
Selbstverständlich kommen Klimamodelle (und auch Eis-Ozean-Modelle) auch dort zum Einsatz, wo das Meereis nicht im Mittelpunkt steht bzw. nur eine Nebenrolle spielt. Beispielsweise sind Änderungen des Meereises für den Klimawandel in den Tropen wenig bedeutsam. In ganzheitlichen Betrachtungen des Klimasystems haben sich interaktive Meereismodelle jedoch als ein wichtiger Baustein von Klimamodellen etabliert. Auch stehen Veränderungen des arktischen Meereises in Verdacht, das Wetter in den mittleren Breiten, einschließlich Europa, zu beeinflussen, was ebenfalls die Bedeutung der Meereismodellierung unterstreicht.
In gekoppelten Klimamodellen ist das Meereis nur einer von vielen wichtigen Aspekten. Während sich der Großteil der für das Klima entscheidenden Physik in der Atmosphäre abspielt, kann das Meereis - je nach wissenschaftlicher Fragestellung - mal eine untergeordnete und mal eine entscheidende Rolle spielen.
Sobald feststeht, welchen Gleichungen ein konkretes Meereismodell grundsätzlich gehorchen soll, gilt es, eine Vielzahl von Parametern festzulegen. So kann eine Annahme sein, dass Eiskristalle, die sich im offenen Wasser bilden, in einer 50 Zentimeter dicken Schicht zusammenfrieren. Warum soll dieser - sogenannte Rinnenschließungsparameter - nicht 20 Zentimeter oder 1 Meter betragen?
Nun könnte man erwarten, dass sich ein solcher Parameter doch einfach in der Natur beobachten und nachmessen lässt. Dabei stellt man jedoch fest, dass dieser Vorgang in Realität sehr unterschiedlich ablaufen kann. Dies hängt wiederum von zahlreichen äußeren Umständen wie z. B. dem Wellengang, der Breite des offenen Wassers, der Temperatur auf komplizierte Art und Weise ab und ist daher sehr schwer zu messen. Man könnte versuchen, diese komplizierten Abhängigkeiten zu berücksichtigen, indem zusätzliche Gleichungen und Größen ins Modell eingeführt werden. Meist würden diese neuen Gleichungen jedoch wiederum neue Parameter enthalten, die ähnlich schwer zu bestimmen sind.
An einem gewissen Punkt muss die Modellentwickler:in sich also mit den verbleibenden Ungenauigkeiten abfinden und bestehende unsichere Parameter festlegen. Dieses Festlegen unterliegt dabei einer gewissen Schätzung. Das betrifft nicht nur den Rinnenschließungsparameter, sondern viele weitere Parameter, zum Beispiel solche, die darüber entscheiden, ab welcher Spannung Brüche im Eis entstehen und wie genau bei der Entstehung von Presseisrücken die Umverteilung von dünneren zu dickeren Eisklassen vonstattengeht. Man kann jedoch aus der Not eine Tugend machen, indem man die Wahl der Parameter davon abhängig macht, wie realistisch die damit erzeugten Simulationen insgesamt sind. Dabei kann man sich an Eigenschaften orientieren, für die vergleichsweise genaue und flächendeckende Beobachtungen vorliegen. Beim Meereis eignet sich dafür die Lage der Eiskante im Verlauf der Jahreszeiten besonders gut. Weitere beobachtbare Zielgrößen, die oft verwendet werden, sind die großräumigen Muster von Eisdicke und Eisdrift.
Diese Vorgehensweise nennt man Modell-Tuning, und die dabei festzulegenden unsicheren Parameter Tuning-Parameter. Ob man dabei manuell vorgeht, also verschiedene Parameter-Kombinationen einzeln ausprobiert und nach Erfahrung und ein Stück weit auch nach Gefühl vorgeht, oder den Optimierungsprozess auf die eine oder andere Art und Weise automatisiert bzw. objektiv gestaltet, liegt dabei im Ermessen der jeweiligen Forschenden. Tatsächlich überwiegt in der Klimaforschung bis heute ein zumindest teilweise manuelles Vorgehen, da automatisierte Vorgehensweisen nicht nur rechentechnisch aufwendig sind, sondern auch dem Anspruch an Objektivität nicht uneingeschränkt gerecht werden können. Ein Beispiel, wo vergleichsweise objektives Tuning von Meereismodellen recht erfolgreich durchgeführt wurde, findet sich in der Studie von Zampieri et al. (2021).
Meereismodelle und Klimamodelle enthalten zwangsläufig vereinfachende Gleichungen und unsichere Parameter und müssen daher optimiert (getuned) werden. Gibt ein Modell selbst nach sorgfältigem Tuning aber wesentliche Aspekte der Realität nicht wieder – zum Beispiel den saisonalen Verlauf der arktische Meereisausdehnung – ist klar, dass das Modell noch nicht „gut“ ist und dass nach Möglichkeit die Modellgleichungen weiterentwickelt werden müssen.
Doch auch ein durch Tuning vermeintlich erfolgreich optimiertes Modell ist nicht automatisch ein gutes Modell. So ist es zum Beispiel möglich, dass ein Modell jene Beobachtungen sehr genau reproduziert, die zum Tuning benutzt worden sind, jedoch große Fehler aufweist, wenn neue Beobachtungen zum Vergleich herangezogen werden. Ein solches Verhalten kann durch Overfitting (Überanpassung) entstehen, und zwar desto leichter, je mehr unsichere Tuning-Parameter ein Modell beinhaltet und je weniger Beobachtungen beim Tuning benutzt werden. In diesem Fall kann es sehr verschiedene Parameter-Kombinationen geben, die beim Tuning ähnlich gut zu funktionieren scheinen.
Es ist also grundsätzlich gut, beim Tuning auf möglichst viele Beobachtungen zurückgreifen zu können. Dies betrifft nicht nur den reinen raumzeitlichen Umfang der Beobachtungen, sondern auch die Berücksichtigung der wichtigsten Größen (z. B. Konzentration, Dicke und Drift) und die Einbeziehung möglichst aller Arten von Zuständen, die mit dem Modell simuliert werden sollen. Soll ein Meereismodell (sei es gekoppelt oder ungekoppelt) beispielsweise für kurzfristige Meereisvorhersagen benutzt werden, ist es hilfreich, wenn die Beobachtungen auch viele ungewöhnliche Ereignisse verschiedenster Art beinhalten, damit sichergestellt werden kann, dass auch diese realistisch wiedergegeben werden. Allerdings ist dabei auch zu berücksichtigen, dass insbesondere Satellitendaten nicht fehlerfrei sind, weshalb Beobachtungen verschiedener Größen nicht notwendigerweise konsistent zueinander sind, was das Tuning zusätzlich verkompliziert.
Geht es um langfristige Klimaprojektionen, kann das letzte Kriterium – die Einbeziehung möglichst aller Arten von Zuständen, die mit dem Modell simuliert werden sollen, beim Tuning – grundsätzlich nicht erfüllt werden. Bei einer solchen Anwendung ist es daher umso wichtiger, dass möglichst wenige unsichere Tuning-Parameter vorhanden sind. Das geht wiederum damit einher, dass die Modellgleichungen zu einem möglichst großen Anteil auf dem festen Grund fundamentaler Physik basieren, statt von Parametrisierungen abzuhängen. Es gilt also die berühmte Einstein zugeordnete Weisheit, man solle die Dinge so einfach machen, wie möglich, aber nicht einfacher. Dabei kommt es auch auf die Anwendung an, für die man das Modell nutzen möchte, wie komplex ein Modell mindestens sein muss; die für die jeweilige Frage wesentlichen Aspekte müssen schließlich Berücksichtigung finden.
In der Praxis ist es nicht immer möglich, unsichere Parametrisierungen durch fundamentale physikalische Gleichungen zu ersetzen. Verbleibende Modell-bedingte Unsicherheiten sind daher unvermeidlich, sei es bei kurzfristigen Meereisvorhersagen oder bei langfristigen Klima- und Meereisprojektionen. Es gibt jedoch vielversprechende Ansätze, die Modelle weiterzuentwickeln und immer „physikalischer“ und dadurch weniger unsicher zu machen. Dabei können drei fundamentale Stoßrichtungen unterschieden werden.
- Es gibt neue Beobachtungen, wie sie beispielsweise bei der MOSAiC-Expedition oder durch neue Satelliten- oder Flugzeugmissionen gewonnen werden, die eine wichtige Rolle spielen. So können Vorgänge besser verstanden und bessere – physikalischere – Parametrisierungen entwickelt werden.
Neue Messdaten, wie sie während der MOSAiC-Expedition gewonnen wurden, sind eine wichtige Grundlage für die Weiterentwicklung von Meereismodellen.
- Mit zunehmenden Rechenkapazitäten ergibt sich die Möglichkeit, immer feinere räumliche Auflösungen, also kleinere Modellgitterzellen, zu verwenden. So können immer größere Anteile beispielsweise der Eisdickenverteilung und der Spannungen und Bewegungen des Eises explizit simuliert werden; die unsicheren Parametrisierungen verlieren dabei an Einfluss. Interessanterweise hat sich in den letzten Jahren gezeigt, dass Strukturen im Meereis – insbesondere größere Rinnen – bei Auflösungen unter etwa 5 km von selbst entstehen, obwohl die von den gröberen Modellen übernommenen dynamischen Gleichungen für solche Strukturen eigentlich nicht ausgelegt sind. Die genauere Untersuchung solcher Phänomene und wie die Modellgleichungen für hohe Auflösungen optimiert werden können, ist ein sehr aktives Forschungsfeld der Meereismodellierung.
- Grundlegend spielt auch immer der Erfindungsgeist der Forschenden eine zentrale Rolle. So können neue Ideen auch ohne zusätzliche Beobachtungen oder schnellere Computer zu besseren Modellen führen, etwa durch neuartige Parametrisierungen oder Innovationen bei den numerischen Methoden.
Box, G. (1979): Robustness in the Strategy of Scientific Model Building, in: Robustness in Statistics, edited by LAUNER, R. L. and WILKINSON, G. N., pp. 201–236, Academic Press. doi.org/10.1016/B978-0-12-438150-6.50018-2
Hibler, W. D. (1979): A dynamic thermodynamic sea ice model. Journal of physical oceanography, 9(4), 815-846.
Rampal, P., Bouillon, S., Ólason, E., & Morlighem, M. (2016): neXtSIM: a new Lagrangian sea ice model. The Cryosphere, 10(3), 1055-1073.
Zampieri, L., Kauker, F., Fröhle, J., Sumata, H., Hunke, E. C., & Goessling, H. F. (2021): Impact of sea‐ice model complexity on the performance of an unstructured‐mesh sea‐ice/ocean model under different atmospheric forcings. Journal of Advances in Modelling Earth Systems, 13, e2020MS002438. doi.org/10.1029/2020MS002438